Phase current control

Controlability

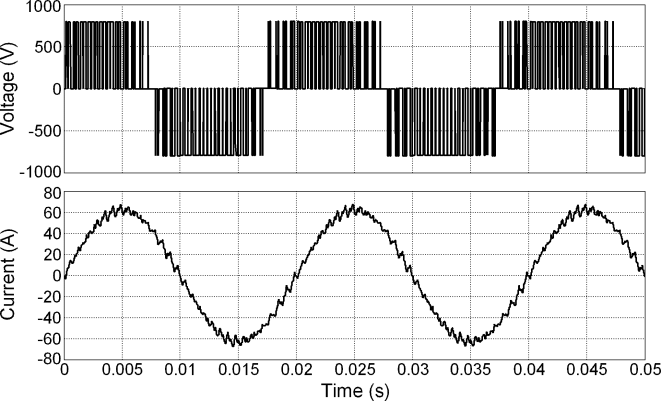
For current control to work properly, certain system conditions must be met. Most importantly, the motor inductance plays a crucial role in successful current control. The rate of current change is directly determined by the inductance and DC voltage according to the following equation:

$\Delta I = \frac{1}{L} \int dU dt$

If we substitute $dU$ with the difference between link voltage and the actual back-EMF, and $dt$ with the duration of 50 microseconds (representing one PWM cycle), we can infer that the current gradient during a single cycle may be high enough to overshoot the current measurement range and trigger short circuit protection. In such a case, we consider the motor to be uncontrollable.

The solution is either:

• to minimize the voltage difference (reduce control error with fine-tuning of the PID loops and the REST algorithm).
• to increase the switching frequency. Switching frequency is fixed for the ESCx families. Please contact us for custom solution.
• to increase inductance (motor redesign with different winding or magnetic material).

It's also important to note that motor inductance is not constant; it tends to decrease as current increases, particularly as the magnetic circuit approaches saturation. This is a common issue with, for example, outrunner motors that lack sufficient magnetic material and reach saturation quickly. In these cases, the motor may become uncontrollable above a certain current threshold.

tip

• To check the dependency of inductance to the motor current, you can use the identsat procedure.

Another critical condition to consider is the impedance of the DC supply, typically a battery. For instance, if the DC resistance is significantly higher than the AC resistance, the control loop may encounter problems. This discrepancy can lead to higher current ripples, which may reduce the lifespan of the electrolytic capacitors and potentially induce hazardous states in the system. The mismatch between DC and AC impedance can compromise the stability and safety of the control system, making it essential to properly account for these characteristics in the design and implementation of the motor control system.

PID

The PID controllers are responsible for adjusting the voltages so that the target current is reached. In BLDC, only a single (scalar) current is treated, whereas in FOC, both torque (Q) and direct (D) axes are controlled separately.

info

• Hereby specified variables are located in the folder /driver/pid_iq resp. /driver/pid_id.
• The PID is abbreviation of 'Proportional-Integral-Derivative' closed loop regulation.
• In the current control loop, only the P- and I- terms are used.

VECTOR

• Q axis: Torque-generating axis
• D axis: Flux-generating axis

BLDC

• BLDC algorithm uses only parameters from pid_iq
• Parameters from pid_id are not used during motor control. It is presented only for the embedded identification procedures (identlin, identrun, ...). Therefore, changing its parameter will not affect motor control performance.

Parameters

Parameters and settings for both pid_iq and pid_id have the same meaning. Usually, the lower the motor inductance, the lower the P and I value should be, and vice versa.

Parameter	Description
P	Proportional term in the PID loop.
I	Integral term in the PID loop.

DTC

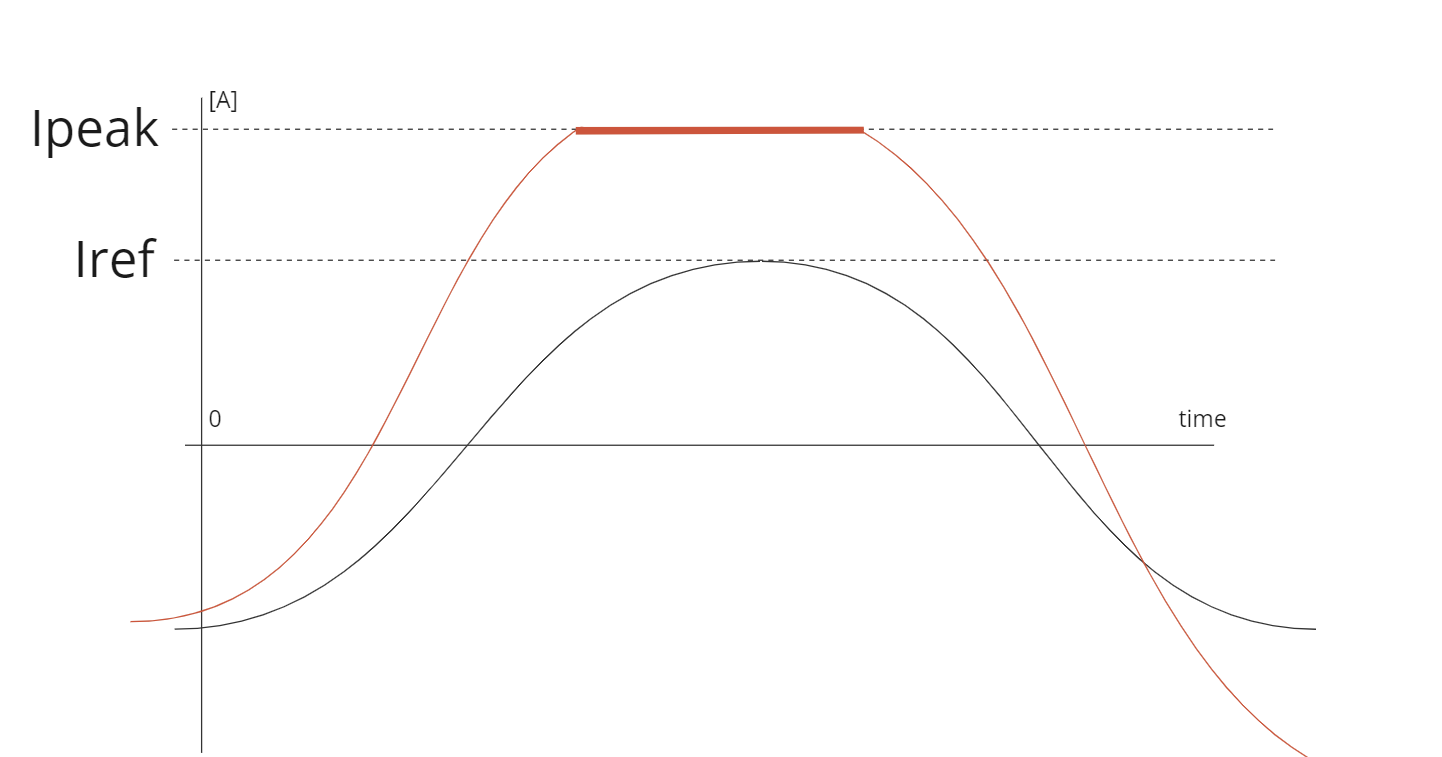
Sometimes, PID controllers may not react quickly enough to meet demanding performance requirements or handle emergency situations like short circuits. If the stator current reaches the current defined by ipeak at any time, even during an ongoing PWM cycle, the system automatically switches to Direct Torque Control (DTC). DTC offers way faster response times and better dynamic performance. This quick-acting alternative helps resolve issues like current overshoots rapidly and effectively prevents various hazardous outcomes in emergency situations. By combining these control methods, the system maintains efficient operation under normal conditions while having the capability to respond swiftly to unexpected challenges, enhancing both performance and safety.

The following picture illustrates the current waveform behavior respective to ipeak and iref under typical circumstances on a single motor phase: